Martin Orr's Blog

Maths > Algebraic geometry > Functor of points

Morphisms and functors of points

Posted by Martin Orr on Thursday, 01 October 2009 at 15:45

This post will discuss the fact that -points of an affine -scheme (and more general objects) are the same as morphisms . James already brought this up in his comment last time. As well as proving this in the affine -scheme case, I shall attempt to give an intuitive explanation of this fact, although I don't find this entirely satisfying.

Morphisms of affine -schemes

In my last post I defined the affine -scheme to have functor of points , but I forget to define morphisms of affine -schemes. This is not hard: you just take natural transformations of the functors. Then the same Yoneda lemma argument as in the case of affine -varieties shows that

In other words, the category of affine -schemes (which I shall write if I ever need to) is equivalent to the opposite of the category of -algebras.

-points as morphisms

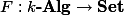
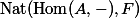
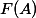
We have not yet got everything we can out of the Yoneda lemma. Recall that the Yoneda lemma says that: for any functor , there is a natural bijection between and . So far we have only applied this in the (very important) special case .

Now let be any functor -- I write instead of because I want to view it as the functor of points of a geometric object. The Yoneda lemma says that

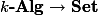
In words, -points of correspond to morphisms .

This formula gives a way of defining the functor of points of an arbitrary -scheme (if you don't know what a -scheme is, for this paragraph you can read it as "object of a nice algebraic-geometric category (over a base field )"). You just take to be the set of morphisms of -schemes .

Note: If you don't think the last paragraph did anything new, previously I had only specified the functor of points for affine objects. We just hoped that "-points" would turn out to make sense for common non-affine objects like schemes. Of course, we really want this construction to induce an equivalence of categories between the category of -schemes and a full subcategory of the category of functors, but I think that proving this takes quite a lot of work.

Interpretation

I want to attempt to justify intuitively why it makes sense that points of should be the same as morphisms (from a certain fixed domain) into .

In the category of sets, there is a bijection between a set and the set of functions from a one-point set to . In the category of topological spaces, there is a bijection between the points of a space and continuous maps from the one-point space to . The same is true in other simple geometric categories, e.g. the category of manifolds or of Riemann surfaces.

In algebraic categories, "one-point space" no longer makes sense (or at least, if you interpret it as meaning the zero object, it doesn't give the right thing). However, it is often possible to choose some other suitable object: for example the elements of an -module biject with -module homomorphisms .

In the case of algebraic geometry, the idea of a "point" becomes more complicated, because we have not just one set of points, but "-points" for each -algebra . But the idea is still that, for each , there is a simple object (namely ) such that -points of are the same as morphisms from this object to .

I don't find this intuition fully satisfying, because is not really a "one-point space" (for example, has two -points), but I suppose that something similar happens in the algebraic case.