Martin Orr's Blog

Maths > Algebraic geometry > Functor of points

Functor of points of non-affine schemes

Posted by Martin Orr on Saturday, 07 November 2009 at 16:59

This post was inspired by Monday's algebraic geometry exercise class, although in fact it fits neatly into my series on functors of points (except that it requires you to know what a scheme is, while previously I have considered only affine schemes). I shall prove the following theorem:

Theorem. There is a canonical bijection between morphisms X \to Y of k-schemes and natural transformations of the corresponding functors of points.

Preliminaries

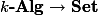
I shall define the functor of points F_X of a k-scheme X to be the functor k\textbf{-Alg} \to \textbf{Set} given by F_X(A) = \mathop{\mathrm{Mor}}(\mathop{\mathrm{Spec}_k} A, X). (\mathop{\mathrm{Mor}} denotes morphisms in the category of k-schemes.)

Note that you can define the functor of points more generally to have domain k\textbf{-Sch}^{\mathrm{op}}; for some purposes this is convenient but to keep with the intuition that "A-points" means "points with coordinates in A" I shall define it only on k\textbf{-Alg} = k\textbf{-AffSch}^{\mathrm{op}}.

If you work with functors of points with domain k\textbf{-Sch}^{\mathrm{op}}, then it is obvious that morphisms between schemes correspond to natural transformations between functors of points; this is just the Yoneda lemma again (as was used in the exercise class for the first two parts of Exercise F).

But when we restrict the domain of functors of points to k\textbf{-AffSch}^{\mathrm{op}}, the theorem is no longer just abstract nonsense. A functor on k\textbf{-AffSch}^{\mathrm{op}} should contain less information than a functor on k\textbf{-Sch}^{\mathrm{op}}, so we have to do some work to show that, if we know that X is the functor of points of some k-scheme, then just knowing X on affine schemes is enough to determine everything. (Note that once we have established the theorem, part 3 of Exercise F follows by abstract nonsense.)

Proof of Theorem

The reason why this theorem is true is of course that k-schemes are covered by affine k-schemes.

So suppose that X is covered by affine k-schemes U_i = \mathop{\mathrm{Spec}_k} A_i. To relate this to points, observe that each inclusion \iota_i : U_i \to X can be seen as an A_i-point of X.

There is an obvious map \alpha : \mathop{\mathrm{Mor}}(X, Y) \to \mathop{\mathrm{Nat}}(F_X, F_Y) = \mathop{\mathrm{Nat}}(\mathop{\mathrm{Mor}}(\mathop{\mathrm{Spec}_k} -, X), \mathop{\mathrm{Mor}}(\mathop{\mathrm{Spec}_k} -, Y)), given by postcomposition, so we just have to show that this is a bijection.

We will need a gluing lemma for morphisms of schemes. The reader should prove this as an exercise. To my surprise I was unable to find it as an exercise in Hartshorne.

Lemma. Let X, Y be k-schemes, and \{ U_i \} an open cover of X.
Suppose that morphisms f_i : U_i \to Y are given for each i, such that f_i |_{U_i \cap U_j} = f_j |_{U_i \cap U_j} for all i and j.
Then there is a unique morphism f : X \to Y such that f |_{U_i} = f_i for all i.

Now to show that \alpha is injective, suppose that \alpha(f) = \alpha(g).

We have that \alpha(f)(\iota_i) = f |_{U_i} \in F_Y(A_i), so \alpha(f) = \alpha(g) gives that f |_{U_i} = g |_{U_i}.

Then the uniqueness part of the lemma tells us that f = g.

And to show that \alpha is surjective, let \tau \in \mathop{\mathrm{Nat}}(F_X, F_Y).

The obvious things to look at now are \tau_{A_i}(\iota_i) \in F_Y(A_i). We consider these as morphisms U_i \to Y, and want to show that they glue to a morphism X \to Y.

To do that, cover U_i \cap U_j by open affines V_{ijk} = \mathop{\mathrm{Spec}}_k C_{ijk} and observe that

\tau_{A_i}(\iota_i) |_{W_{ijk}} = \tau_{C_{ijk}}(\iota_i |_{W_{ijk}}) = \tau_{C_{ijk}}(\iota_j |_{W_{ijk}}) = \tau_{A_j}(\iota_j) |_{W_{ijk}}.

So by uniqueness of gluing, \tau_{A_i}(\iota_i) |_{U_i \cap U_j} = \tau_{A_j}(\iota_j) |_{U_i \cap U_j}, and hence we can indeed glue all the \tau_{A_i}(\iota_i) together.

Tags alg-geom, maths, points-func

Trackbacks

No trackbacks.

Comments

  1. Arne Smeets said on Sunday, 08 November 2009 at 01:14 :

    The lemma you are stating is already one of the remarks in section 2.1 of Harari's notes :)

  2. Martin Orr said on Sunday, 08 November 2009 at 14:32 :

    So it is! I shall remove the reference to Harari's Lemma 2.21 then.

  3. Arne Smeets said on Sunday, 08 November 2009 at 15:07 :

    Good idea, since this lemma is easily proved without the "heavy" glueing lemma.

Post a comment

Markdown syntax with embedded LaTeX.
Type LaTeX between dollar signs, and enclose them between backticks to protect it from Markdown.
All comments are subject to moderation before they appear on the blog.

Topics