Martin Orr's Blog

Maths > Algebraic geometry > Hensel's lemma

Ordinary multiple points

Posted by Martin Orr on Monday, 10 May 2010 at 21:41

Singular points in a curve are places where curve fails to be smooth: intuitively, multiple points of the curve pile up on top of each other. In this post I will describe a simple invariant of curve singularities, the multiplicity, which essentially counts how many points are piled up there. In the simplest case of an ordinary multiple point, I describe how to use the previous post's algorithm to compute a power series for each branch of the curve near the singularity.

Defining multiplicity

In the case of , intuition suggests that the origin lies on this curve "twice": there are two "branches" passing through the origin, and if we could look at each branch separately, the origin should be a smooth point of that branch.

One way of justifying this is to say that, for and small, the dominant terms of the equation are the quadratic ones: . This factorises as , and the lines , are the tangents to the two branches of .

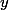
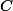
In general, we define the multiplicity of a curve at to be the lowest total degree of a non-zero term in (by "total degree" I mean the sum of the and degrees).

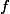
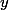
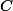
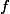
The curve is approximated near the origin by the curve whose equation is obtained by picking all the total-degree terms of and throwing away the rest.

This gives a homogeneous polynomial of degree , which (over an algebraically closed field) splits as a product of linear factors - in other words the curve is just a union of lines through the origin. To find the factors, set and decomposing the resulting one-variable polynomial . (This one-variable polynomial might have degree less than , but in this case the missing factors of are factors of ).

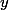
The tangent lines to 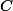at are the lines defined by the linear factors of . We see that there are at most tangent lines. There may be fewer tangent lines if some are repeated - for example which has multiplicity 2, with the line appearing as a tangent line twice.

A singular point with no tangent lines repeated - i.e. it has multiplicity and distinct tangent lines is called an ordinary multiple point.

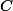
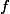
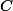
Recall that a point on is non-singular iff at least one of , is non-zero. In other words, the origin is non-singular iff has a non-zero degree 1 term. Hence a point on is non-singular if and only if its multiplicity is exactly 1.

Furthermore, at a non-singular point, the tangent line defined above is the same as the usual tangent line.

Intersection multiplicities

Here is another, more geometric, way of defining the multiplicity of a point on a plane curve.

We first define the intersection multiplicity between a curve and a line.

Suppose that is the line and the curve , passing through the origin. Substitute in to get the one-variable polynomial . Then the intersection multiplicity between and at is the multiplicity of as a root of this polynomial.

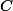
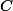
If is the -axis, we need to substitute in instead.

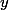
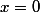
We see that the intersection multiplicity is a positive integer, at most the degree of .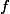

Furthermore, the intersection multiplicity between and at is always at least , the multiplicity of on , because only terms of degree at least can appear in .

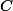
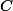
The intersection multiplicity is greater than if and only if the total-degree terms of vanish: in other words iff is a linear factor of the polynomial obtained by picking out the total degree terms of . (This works also for .)

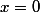
We conclude that: the multiplicity of on is the minimum (over all lines through ) of the intersection multiplicities of with at ; the intersection multiplicity is equal to the multiplicity of on for all but finitely many lines ; and the exceptional lines are precisely the tangents to at .

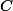
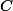
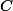
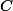
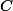
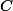
In the simplest case, a tangent line has intersection multiplicity with at one greater than the multiplicity of in . This may fail to hold even at an ordinary multiple point, indeed even at a non-singular point, such as the origin on the curve . Conversely, a point may fail to be ordinary while all its tangents still have intersection multiplicity one greater than the multiplicity of the point: for example at the origin of , the only tangent is the -axis with intersection multiplicity 3.

Solving for power series at an ordinary multiple point

In the previous post I gave an algorithm for constructing a power series solution to a polynomial at a non-singular point where the curve does not have a vertical tangent. Today I shall consider an ordinary point of multiplicity which does not have a vertical tangent. For simplicity suppose that the chosen point is the origin.

Obviously we cannot get a unique power series expansion for 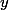, because there should be one for each branch. So we begin by picking a branch, with tangent .

A power series expansion along this branch will have the form . We can remove a factor of and write ; then we are looking for a power series satisfying (this replacing of by is an example of the important process of blowing up).

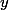
The polynomial has a factor of ; say . The is irrelevant to finding a power series expansion for , so we focus on .

Let . This polynomial is formed from the total-degree r terms of , and its roots are the gradients of the tangents to .

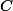
Since our point is an ordinary multiple point, these roots are distinct. So we can apply the algorithm of the previous post to find a unique power series satisfying .

For example, let , and choose the branch with gradient +1. We get , and the power series for this branch of the original curve is