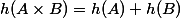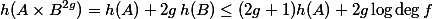Maths > Abelian varieties > The Masser-Wüstholz isogeny theorem
The Masser-Wüstholz isogeny theorem
Posted by Martin Orr on Wednesday, 25 April 2012 at 14:09
Let 





The Masser-Wüstholz isogeny theorem answers this question, at least subject to a minor condition on polarisations (I think that this was removed in a later paper of Masser and Wüstholz but it is not too important anyway -- when deducing Finiteness Theorem I you can remove the polarisation issue with Zarhin's Trick).
Theorem. (Masser, Wüstholz 1993) Let
andbe principally polarised abelian varieties over a number field. Suppose that there exists some isogeny. Then there is an isogenyof degree at mostwhereandare constants depending only on the dimension of.
We will prove this using the Masser-Wüstholz period theorem which I discussed last time.
Proof of the isogeny theorem
Recall from last time that in order to obtain an isogeny of bounded degree between a subvariety of 

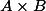


Actually we will construct a non-split subvariety 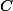
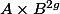
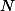
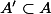
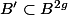
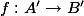
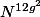
If we suppose that 
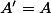
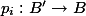
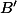
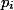
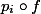
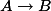
If 
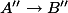
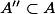
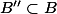
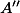
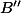
Finding a non-split subvariety
It remains to show that for any isogenous abelian varieties 

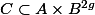
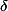
![[K:\mathbb{Q}]](http://www.martinorr.name/blog/images/mathtex/1216.png)
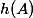
Choose a non-zero period 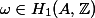
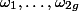
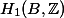
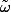
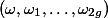
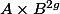
Let 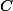
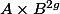
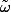
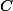


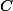
To prove the latter, let 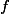
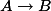
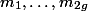
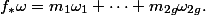
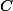
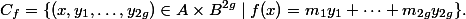
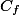

(Observe that the degree of 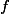
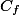
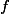
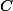
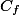
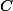
Bounding the degree of the subvariety
The period theorem tells us that
![\deg_{\lambda \times \mu^{2g}} C \leq c \max([k:\mathbb{Q}], h_F(A \times B^{2g}), H(\tilde{\omega}, \tilde{\omega}))^\kappa](http://www.martinorr.name/blog/images/mathtex/1226.png)
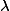
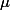



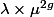
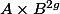
We want to remove 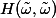
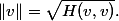
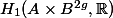
We have
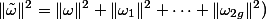

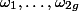
The only condition that we have put on 
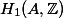
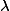
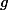
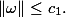
With regard to 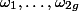
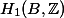
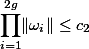
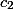
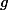
An upper bound for the product 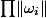
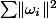
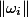
Lemma. Let
be a principally polarised abelian variety defined over a number field. There is a constantdepending only onsuch that every non-zero periodofsatisfies
Finishing the proof
Combining the above, we get that the isogeny 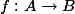
![\deg f \leq c \max([K:\mathbb{Q}], h_F(A \times B^{2g}))^\kappa.](http://www.martinorr.name/blog/images/mathtex/1243.png)

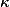
However this bound depends on 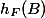
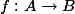
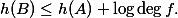
![\deg f \leq c \max([K:\mathbb{Q}], h(A) + \log \deg f)^\kappa.](http://www.martinorr.name/blog/images/mathtex/1246.png)
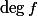
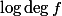
![c \max([K:\mathbb{Q}], h(A))^\kappa](http://www.martinorr.name/blog/images/mathtex/1196.png)
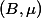
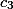
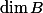
![\lVert \omega \rVert_\mu \geq c_3 ([K:\mathbb{Q}] h(B))^{-1/2}.](http://www.martinorr.name/blog/images/mathtex/1242.png)
"Any subvariety of
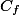


Right at the end, "So we get that...": Are you claiming that
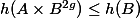
No. I use that
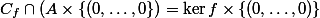
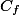
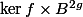
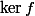
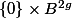

Again no. I confusingly left out some steps. We use the fact that