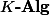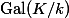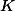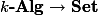Posts tagged points-func | Martin Orr's Blog

Galois descent for morphisms of functors of points

Posted by Martin Orr on Saturday, 20 February 2010 at 21:58

I was disappointed in my last post that I was unable to prove any results about Galois descent for morphisms of functors. I have now tracked down a fairly mild condition on the functors that you need for this descent to work, which I shall explain below. Importantly, this condition is satisfied automatically by the functors of points of a scheme (though I won't prove this).

This tells us that if you have two -functors satisfying the Galois exactness property, and a morphism of their restrictions to which commutes with the action of , then it comes from a unique morphism of -functors.

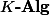
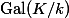
I shall not discuss descending functors, only morphisms. But a small modification to the Galois exactness condition should allow you to descend functors themselves.

no comments Tags alg-geom, descent, maths, points-func Read more...

Galois ascent for functors of points

Posted by Martin Orr on Thursday, 04 February 2010 at 22:10

I was very pleased this weekend when I worked out how to define Galois descent data for functors of points. I was less pleased when I reached the end of this post and discovered that I couldn't prove that descending morphisms of functors works nicely.

Galois descent relates objects (e.g. vector spaces, varieties) defined over a field to objects defined over a bigger field with "descent data": a "semilinear" action of on the -object.

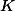
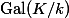
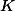
If we want to do this for functors of points, it is not clear how to define a semilinear morphism. That is what I shall explain in this post, together with how to ascend (go from a functor over the small field to one over the big field). This is all purely formal.

no comments Tags alg-geom, descent, maths, points-func Read more...

Functor of points of non-affine schemes

Posted by Martin Orr on Saturday, 07 November 2009 at 16:59

This post was inspired by Monday's algebraic geometry exercise class, although in fact it fits neatly into my series on functors of points (except that it requires you to know what a scheme is, while previously I have considered only affine schemes). I shall prove the following theorem:

Theorem. There is a canonical bijection between morphisms of -schemes and natural transformations of the corresponding functors of points.

3 comments Tags alg-geom, maths, points-func Read more...

Functors of points and base ring

Posted by Martin Orr on Thursday, 08 October 2009 at 09:58

So far in my series on functors of points, I have considered functors for some fixed field . We begin by observing that we may allow to be any ring. Then I consider whether it is possible to relate functors with base ring to functors with base ring , with only partial success.

no comments Tags alg-geom, maths, points-func Read more...

Morphisms and functors of points

Posted by Martin Orr on Thursday, 01 October 2009 at 15:45

This post will discuss the fact that -points of an affine -scheme (and more general objects) are the same as morphisms . James already brought this up in his comment last time. As well as proving this in the affine -scheme case, I shall attempt to give an intuitive explanation of this fact, although I don't find this entirely satisfying.