Maths > Algebraic geometry > Hensel's lemma
Hensel's lemma and algebraic functions
Posted by Martin Orr on Monday, 05 April 2010 at 22:34
An algebraic function is a function which we obtain by solving a polynomial in two variables 
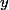
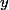

I shall give an algorithm for expressing an algebraic function (in such a nicely behaved region) as a power series, thereby proving that a power series solution to the original polynomial exists. The generalisation of this result to a complete discrete valuation ring is Hensel's lemma, and is particularly important to number theorists in the case of p-adic integers (which were invented by Hensel). In this post I will focus on the case of algebraic functions, as it is easier to apply geometric intuition.
Algorithm for constructing power series
Suppose we have a polynomial ![f(x, y) \in \mathbb{C}[x, y]](http://www.martinorr.name/blog/images/mathtex/543.png)

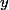

Of course, in general there will be several values of 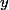

Consider a value 



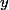


Of course it is not obvious that the function 


For example, take 
Then 

So there should be a unique power series 

To find it, we can solve for 
-
Try






-
Try






-
Try








Continuing in this way, we build up the power series

The graph to the right shows that the first four terms of this power series approximate the curve 

Proof that the algorithm works
Now we shall prove that the algorithm does construct a power series 

At each step we are setting 


By induction, we have chosen 







We need to show that there is a unique value for 






If we let 







(Note: it is perhaps wrong to call this an "algorithm" since it doesn't terminate. It can't terminate because it is constructing an infinite object, a power series. But in finite time it will give us any particular term of the power series.)
Hensel's lemma
The above algorithm gives a constructive proof of:
Hensel's lemma. Let 
![\mathbb{C}[x, y]](http://www.martinorr.name/blog/images/mathtex/580.png)


![y(x) \in \mathbb{C}[[x]]](http://www.martinorr.name/blog/images/mathtex/581.png)


Note that the lemma is entirely asymmetric between 
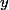
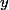
![\mathbb{C}[x]](http://www.martinorr.name/blog/images/mathtex/584.png)
![\mathbb{C}[[x]]](http://www.martinorr.name/blog/images/mathtex/585.png)
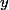
![\mathbb{C}[[x]]](http://www.martinorr.name/blog/images/mathtex/585.png)

If you know what a complete discrete valuation ring is, you can observe that the algorithm works for polynomials over any complete DVR (the function 

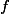

![A[y]](http://www.martinorr.name/blog/images/mathtex/588.png)