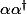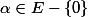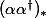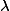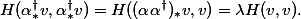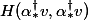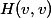Maths > Abelian varieties > Endomorphisms of abelian varieties
Rosati involutions
Posted by Martin Orr on Wednesday, 05 December 2012 at 16:04
I intend to return to the basic theory of abelian varieties and write write a few posts on their endomorphism algebras and associated moduli spaces. To begin with, I will discuss the Rosati involution which is an involution of the endomorphism algebra coming from a polarisation. The existence of such an involution is crucial for the classification of endomorphism algebras which I will discuss next.
Involutions and bilinear forms
To motivate the definition of the Rosati involution, we will begin by considering the correspondence between bilinear forms on a vector space and anti-automorphisms of its endomorphism algebra. This correspondence is also used in the classification of algebras with involution.
Let 
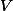


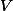




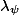

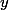

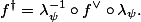
This defines an anti-automorphism of the matrix algebra 

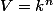


Theorem. The map sending a bilinear form to its adjoint anti-automorphism is a bijection between
- equivalence classes of nonsingular bilinear forms on
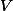
- anti-automorphisms of

The main thing to be proved is that every anti-automorphism comes from some bilinear form.
This relies on the Skolem-Noether theorem, that every automorphism of 
We say that an anti-automorphism is an involution if its square is the identity. Under the bijection, a bilinear form corresponds to an involution if and only if it is either symmetric or alternating.
The Rosati involution
Let 



We can therefore apply the same formula as in linear algebra to define an involution of the endomorphism algebra:
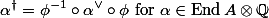


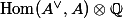


If we look at homology, either the 
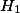

Positivity of the Rosati involution
Let 

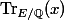

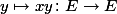
The Rosati involution is a positive involution, meaning that
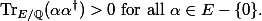
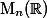

Hence the positivity of the Rosati involution says that if we think of the polarisation as being "like a bilinear form", then it is "positive or negative definite" (but -1 times a polarisation is not a polarisation, so we can treat polarisations as always being "positive definite").
The general proof that the Rosati involution is positive (valid over all fields, including those of positive characteristic) uses étale cohomology to show that 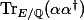
Let 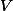


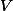




Lemma. If
, then all eigenvalues ofonare nonnegative real numbers, and at least one is positive.Proof. Let
be an eigenvector ofwith eigenvalue. ThenBecauseis positive definite,is a nonnegative real number andis a positive real number, sois a nonnegative real number.
Now consider 
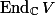
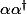
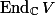
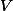
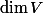
Finally 
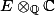
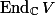

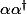
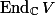
We note also that 





The trace of