Maths > Algebraic geometry > Functor of points
Galois ascent for functors of points
Posted by Martin Orr on Thursday, 04 February 2010 at 22:10
I was very pleased this weekend when I worked out how to define Galois descent data for functors of points. I was less pleased when I reached the end of this post and discovered that I couldn't prove that descending morphisms of functors works nicely.
Galois descent relates objects (e.g. vector spaces, varieties) defined over a field 

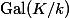

If we want to do this for functors of points, it is not clear how to define a semilinear morphism. That is what I shall explain in this post, together with how to ascend (go from a functor over the small field to one over the big field). This is all purely formal.
Galois descent for vector spaces
Here is a quick reminder of Galois descent for vector spaces. For more details and proofs, see Keith Conrad's notes.
Throughout this post, 

Given a 
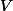


This action is not 






Furthermore, given a 





The above ("ascent") is all formal in nature.
Descent (which you have to work to prove) tells you that given a 






Semilinear morphisms of functors
I shall write "



Let 




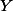

As is the case with vector spaces, a 




Hence we cannot tweak the definition of a "morphism" 
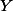


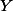

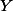
Twisted 

Given a 






Now 


Note that 






The importance of the functor 

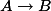


Twisted 

Given a 




This takes affine 



so 
Now we can define a 



(In the affine case, this corresponds to a 


A semilinear action of 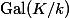







(


Ascending 

Let 






To get a semilinear action of 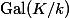







This is a bit weird: we get a non-trivial group action by leaving the points on which 
Descending morphisms of 

That was a lot of formal manipulation, for which I am going to give no immediate pay-off. The point is that it gives us the language we need to think about descent, which is much less trivial than ascent (indeed, it is not always possible to descend: you have to impose conditions on the descent data).
However, what I really wanted was to be able to descend morphisms of 
I wanted to show that, if 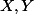



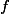


Unfortunately I can't prove this, and it looks like it might be false without some condition on