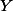Martin Orr's Blog

Maths > Algebraic geometry > Functor of points

Galois descent for morphisms of functors of points

Posted by Martin Orr on Saturday, 20 February 2010 at 21:58

I was disappointed in my last post that I was unable to prove any results about Galois descent for morphisms of functors. I have now tracked down a fairly mild condition on the functors that you need for this descent to work, which I shall explain below. Importantly, this condition is satisfied automatically by the functors of points of a scheme (though I won't prove this).

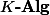
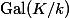
This tells us that if you have two k-functors satisfying the Galois exactness property, and a morphism of their restrictions to K\textbf{-Alg} which commutes with the action of \mathop{\mathrm{Gal}}(K/k), then it comes from a unique morphism of k-functors.

I shall not discuss descending functors, only morphisms. But a small modification to the Galois exactness condition should allow you to descend functors themselves.

I shall use notation from my previous post setting up the framework for Galois descent of functors.

Throughout this post, K/k will denote a Galois field extension, with Galois group G. If B is a k-algebra, I shall write B_K for B \otimes_k K, given the structure of a K-algebra through the right-hand factor.

Galois exactness

If X is a k-functor, then I shall write X_K for the K-functor obtained by composing X with the forgetful functor K\textbf{-Alg} \to k\textbf{-Alg}.

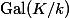
Recall that X_K comes with a semilinear \mathop{\mathrm{Gal}}(K/k)-action (\phi_\sigma) -- in fact this is just given by identity maps, but I would prefer to keep the action explicit as I tend to think about (X_K, \phi_\sigma) as only defined up to a canonical isomorphism of K-functors with K/k-action.

For every k-algebra B, there is a homomorphism of k-algebras \Delta : B \to B \otimes_k K given by b \mapsto b \otimes 1. There are also homomorphisms (of K-algebras) \sigma_B : B_K \to F_\sigma(B_K) given by b \otimes x \mapsto b \otimes \sigma(x) for each \sigma \in G.

These homomorphisms have the property that if we identify B_K and F_\sigma(B_K) in the "trivial" way (as k-algebras but only semilinearly as K-algebras), then \Delta is the equalizer of the \sigma_B in the category k\textbf{-Alg}.

I shall call the k-functor X Galois exact if, for every k-algebra B, X(\Delta) is the equalizer (in \textbf{Set}) of \phi_\sigma \circ X(\sigma_B) : X(B_K) \to X(B_K); in other words

  1. X(\Delta) is injective, and
  2. The image of X(\Delta) is X(B_K)^G := \{ x \in X(B_K) : \phi_\sigma(X(\sigma_B)(x)) = x \text{ for all } \sigma \in G \}.

An important fact is that the functor of points of a k-scheme is always Galois exact. To prove this, you need to do some geometry to reduce to the affine case.

Descending morphims of functors

Now let X, Y be two k-functors and \tilde{f} a natural transformation X_K \to Y_K. We need to assume that Y is Galois exact.

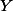
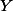
I want to show that, if \tilde{f} commutes with the Galois action, then there is a unique morphism of k-functors f : X \to Y extending \tilde{f}.

I will say that \tilde{f} commutes with the Galois action if the following diagram commutes for all K-algebras B and \sigma \in G:

\usepackage{xypic} \xymatrixcolsep{4pc} \xymatrix{ {X(F_\sigma(B))} \ar[d]^{X(\sigma_B)} \ar[r]^{\tilde{f}(F_\sigma(B))} & {Y(F_\sigma(B))} \ar[d]^{Y(\sigma_B)} \\ {X(B)} \ar[r]^{\tilde{f}(B)} & {Y(B)} }

To construct 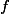f, consider the following diagram for each k-algebra B:

\usepackage{xypic} \xymatrixcolsep{3pc} \xymatrix{ {X(B_K)} \ar[r]^{\tilde{f}(B_K)} & {Y(B_K)} \\ {X(B)} \ar[u]^{X(\Delta)} \ar@{.>}[r]^{f(B)} & {Y(B)} \ar[u]^{Y(\Delta)} }

Because \tilde{f} commutes with the Galois action, \tilde{f}(B_K) \circ X(\Delta) is unchanged by postcomposition with \phi_\sigma \circ Y(\sigma_B) for each \sigma \in G. So by the Galois exactness of Y, there is a unique f(B) making the diagram commute.

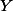
Proving that this really is descent

To check that f_K = \tilde{f}, we need to check that if B is a K-algebra, then the above diagram commutes when \tilde{f}(B) is put in place of the bottom arrow.

This is not an immediate consequence of the fact that \tilde{f} is a natural transformation because \Delta is not a homomorphism of K-algebras. Instead consider the following diagram, where \mu : B_K \to B is the K-algebra homomorphism b \otimes x \mapsto bx:

\usepackage{xypic}\xymatrixcolsep{3pc}\xymatrix{ & {X(B_K)} \ar[d]^{X(\mu)} \ar[r]^{\tilde{f}(B_K)} & {Y(B_K)} \ar[d]^{Y(\mu)} \\ {X(B)} \ar[ur]^{X(\Delta)} \ar[r]^{\mathop{\mathrm{id}}} & {X(B)} \ar[r]^{\tilde{f}(B)} & {Y(B)} }

The triangle commutes because \mu \circ \Delta = \mathop{\mathrm{id}_B}, and the square commutes because \tilde{f} is a natural transformation of K-functors. Hence the outer trapezium commutes.

Since Y is Galois exact, the restriction of Y(\mu) to Y(B_K)^G is a bijection Y(B_K)^G \to Y(B), with inverse Y(\Delta). Since \tilde{f} is Galois exact, the image of \tilde{f}(B_K) \circ X(\Delta) is contained in Y(K_B)^G. Combining these, we get that the required diagram commutes.

Tags alg-geom, descent, maths, points-func

Trackbacks

No trackbacks.

Comments

No comments.

Post a comment

Markdown syntax with embedded LaTeX.
Type LaTeX between dollar signs, and enclose them between backticks to protect it from Markdown.
All comments are subject to moderation before they appear on the blog.

Topics