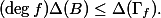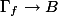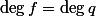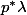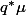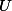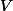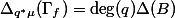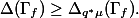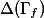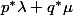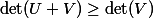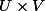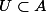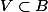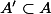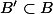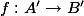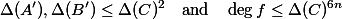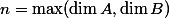Maths > Abelian varieties > The Masser-Wüstholz isogeny theorem
The Masser-Wüstholz period theorem
Posted by Martin Orr on Friday, 30 March 2012 at 12:20
I wanted to write a post about the Masser-Wüstholz isogeny theorem, which gives a quantitative version of Finiteness Theorem I. But it turned out to be too long so for today I will focus on the main ingredient in the proof of the isogeny theorem: the Masser-Wüstholz period theorem.
The period theorem gives a bound for the degree of the smallest abelian subvariety of a fixed abelian variety 

Period Theorem. (Masser, Wüstholz 1993) Let
be an abelian variety defined over a number fieldwith a principal polarisation. For any non-zero periodof, the smallest abelian subvarietyofwhose tangent space containssatisfieswhereandare constants depending only on.
Masser and Wüstholz gave a value for 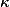
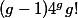
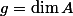
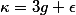
Periods
Let 
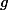
A period of 
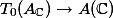


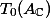
One of the ways of interpreting a polarisation is as a positive definite Hermitian form 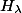
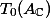
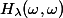
The degree of a polarised abelian variety
Let 

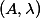
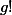
First we define what Masser and Wüstholz call the normalised degree 

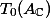
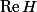
An equivalent way of defining the normalised degree is as the square root of the degree of 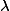

The unnormalised degree 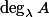
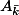
The two degrees are related by the Riemann-Roch theorem for abelian varieties:
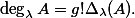
For our purposes it will be convenient to work always with the normalised degree. I stated the period theorem with the unnormalised degree because that is the standard statement, but of course we can replace it by the normalised degree if we want.
The degree of the graph of an isogeny
Let 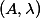
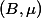
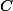
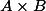
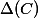
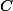
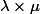
Note that 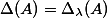
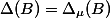
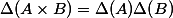
Suppose that there is an isogeny 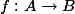
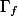
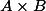
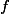
Lemma.
Proof. Let
,be the projectionsand. Note thatis an isomorphism and.We get polarisations
andon. Let,be the real parts of the associated Hermitian forms, which we may interpret as positive-definite symmetric matrices.We have
so it will suffice to prove thatRecall that
means the degree ofwith respect to the restriction of, which is given by. So we haveThus the lemma follows from the fact that
for any positive-definite symmetric real matricesand. This inequality is left as an exercise for the reader.
From subvarieties to isogenies
When can we reverse the process of going from an isogeny to its graph?
That is, when does an abelian subvariety of 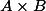
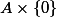
Definition. We say that a subvariety of
is split if it has the formfor someand.
Suppose that there is a non-split abelian subvariety 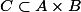


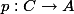
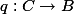


We would like to show that there is an isogeny 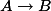
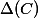
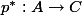
![p^* \circ p = [\deg p]](http://www.martinorr.name/blog/images/mathtex/1296.png)
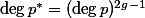
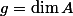
By the above lemma, 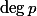
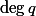
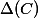
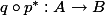
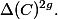
Dropping the assumption that 

Lemma. If
has a non-split abelian subvarietythen there are non-zero abelian subvarietiesandand an isogenysuch thatwhere.


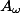
![\deg_\lambda A_\omega \leq C \max([k:\mathbb{Q}], h_F(A), H_\lambda(\omega, \omega))^\kappa](http://www.martinorr.name/blog/images/mathtex/1256.png)