Martin Orr's Blog

Maths > Algebraic geometry > Functor of points

The functor of points of an affine variety

Posted by Martin Orr on Tuesday, 25 August 2009 at 20:56

I think I have made some progress recently in understanding the "functor of points" idea in algebraic geometry. In this article I shall explain how the functor of points of an affine variety arises simply by considering solutions to fixed polynomials over varying rings; this gives the motivating example for considering functors associated to more general algebraic-geometric objects.

Of course, the starting point for algebraic geometry is to look at solutions to polynomial equations, for example . If we work over an algebraically closed field , then we can just consider an affine -variety to be the set of solutions to some polynomials and everything works nicely (because, in particular, we can use the Nullstellensatz).

As an arithmetic geometer however, I am interested in solutions to equations over fields which are not algebraically closed fields, or even over rings which are not fields. For example, the question of what solutions has over or is much more interesting than over .

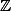
Here, even if an equation is defined over some field , just considering its solutions over that field is not enough. For example, there are many affine plane curves defined over whose only rational point is , but these are not all isomorphic. They may have different points over , and we care about these extra points (for example we may want to consider points defined over number fields on the way to working out what the rational points of a given elliptic curve are).

So in considering the algebraic-geometric object defined by an equation, we need to consider the sets of solutions over many different fields. In fact it turns out that we should consider rings as well as fields (I don't have a simple explanation for why this is the case). If is any -algebra, then a polynomial with coefficients in makes sense over . Given some polynomials over defining an affine variety , we shall write for the set of solutions to these polynomials over , and call them the -points of .

Furthermore if a -algebra is contained in another -algebra , then every -point of an affine variety gives rise to a -point (e.g. a real solution to is also a complex solution). More generally a -algebra homomorphism induces a map . In other words, we have a functor from the category of -algebras to the category of sets.

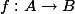
So associated to an affine -variety is a functor which tells you, for each -algebra , the "set of points of defined over ." This functor determines the variety (I will probably prove this in my next post on the subject).

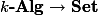
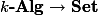
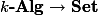
The idea behind the functor of points approach is that the same thing will work for objects much more general than affine varieties e.g. schemes, algebraic spaces: associated to each object is a functor . You still think of this functor as meaning "points defined over ", even though the "points" may not be quite so concrete as in the case of affine varieties. In fact, one can even turn this round and think of arbitrary functors as algebraic-geometric objects; affine varieties or schemes are then just special functors.

The reason (or at least, a reason) why this is useful is that often the easiest way to define a new algebraic-geometric object is just to specify what its points over are for each -algebra . Then you prove afterwards that this functor satisfies the conditions for being a scheme or projective or whatever.

To conclude, the idea is that algebraic-geometric objects (defined over ) are really just objects that have a set of points for each -algebra, and the functor of points is a way of writing this down. In principle you can get all the other information, like Zariski topology and structure sheaves, out of the functor of points, but it's quite a lot of work.