Maths > Algebraic geometry > Functor of points
Functors, affine varieties and Yoneda
Posted by Martin Orr on Wednesday, 02 September 2009 at 22:51
In this article, I will examine in more detail the functor of points of an affine variety,
which I defined in the last article.
I shall show that this functor is the same as a Hom-functor on the category of 
Points of an affine variety and Hom-functors
First we give a categorical description of the functor of points of an affine variety.
Recall that the category of affine 





Hence there is one obvious choice of (covariant) functor 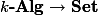

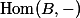

Lemma 1. For every
-algebra, there is a bijection between-points ofand elements of(where the Hom is in the category of-algebras).Proof. This is just a matter of unpacking definitions.
First we unpack "the
-points of".Suppose that
is embedded in affine-space over.Then
is defined by an idealin, and the-points ofare those points inat which all polynomials invanish.Furthermore,
. So we have to prove:Claim. There is a bijection between points of
at which all polynomials invanish, and elements of.Now a
-algebra homomorphismis determined by givingelements of, namely. This gives a bijection betweenand(the caseof the claim).And all the polynomials in
vanish at a given point iniffis contained in the kernel of the corresponding homomorphism, establishing the claim.End of proof.
This shows that the functor of points of 
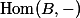
Morphisms and natural transformations
Now we discuss morphisms. The obvious definition of a morphism between two functors is a natural transformation. We shall prove that in fact, morphisms between affine varieties are the same as natural transformations between their functors of points. The tool we use to do this is the Yoneda lemma (this proof illustrates a general method of applying the Yoneda lemma).
Let 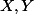

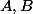
The Yoneda lemma tells us that for any functor 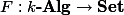
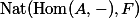
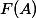
In particular, taking 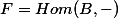


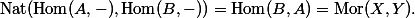
Since 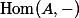
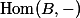

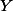

Note that this fact as an important corollary:
If two affine 
Thus we have seen that the functor of points of an affine variety has a simple categorical description, and that we can easily describe morphisms between affine varieties via the functors. This suggests that an approach to algebraic geometry based on functors of points is not just going to make things hopelessly complicated.

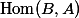
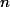
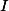
![k[x_1, \ldots, x_n]](http://www.martinorr.name/blog/images/mathtex/247.png)
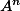
![B = k[x_1, \ldots, x_n] / I](http://www.martinorr.name/blog/images/mathtex/249.png)
![\mathop{\mathrm{Hom}}(k[x_1, \ldots, x_n] / I, A)](http://www.martinorr.name/blog/images/mathtex/250.png)
![f : k[x_1, \ldots, x_n] \to A](http://www.martinorr.name/blog/images/mathtex/251.png)
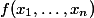
![\mathop{\mathrm{Hom}}(k[x_1, \ldots, x_n], A)](http://www.martinorr.name/blog/images/mathtex/253.png)
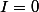
![k[x_1, \ldots, x_n] \to A](http://www.martinorr.name/blog/images/mathtex/255.png)