Functors of points and base ring
Posted by martin on Thursday, 08 October 2009 at 09:58
So far in my series on functors of points, I have considered functors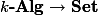 
for some fixed field 
. We begin by observing that we may allow to be any ring. Then I consider whether it is possible to relate functors with base ring to functors with base ring 
, with only partial success.
Functors over rings
So far, I have only defined the functor of points of an algebraic-geometric object defined over to be a functor where is some field. (For convenience, I shall call this a -functor in this post.) However, if you look carefully, you will see that we have never used the fact that is a field. Hence we may consider a functor 
where 
is any ring, and view it as the functor of points of an object defined over .
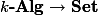
Recall that the basic example of a -functor is an affine -scheme 
. This tells you the sets of solutions in a varying -algebra to some fixed polynomials with coefficients in . The same thing is true for -functors: an affine -scheme is defined by some polynomials with coefficients in , and the functor of points tells you their solutions over all -algebras.
This is not just generalisation for the sake of it. For example, suppose we have a polynomial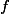 
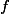
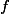
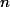
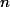
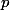
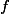
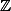
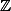
with integer coefficients. In order to understand integer solutions to , it is often useful to consider mod 
for various (or over the 
-adics), as well as looking at over 
or extensions thereof. This means that it is not enough to consider the corresponding affine -scheme 
, because the functor of points of is only defined on 
and 
is not a -algebra in any way. However is a -algebra, so the functor of points of the corresponding affine -scheme contains all this useful information.
Changing the base ring
In the locally-ringed spaces approach to algebraic geometry, you define a -scheme to be a -scheme 
together with a morphism 
. So the question arises, is this description valid for functors? More precisely, is a -functor the same as a -functor together with a natural transformation to 
?
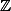
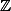
Because functors are much more general than schemes, there is no particular reason to assume that this should be true. In fact there is a simple map { 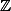-functors with morphisms to } 
{ -functors }, but I cannot find any map in the reverse direction.
To construct this map, suppose we have a functor 
and a natural transformation 
. We want to define a functor 
.
Suppose that 
is a -algebra (where 
is the defining homomorphism 
). The easy way to see what 
should be is to view 
-points of as morphisms 
, as in the last post. Then -points of 
are those morphisms such that the following diagram commutes:
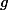
![$ \usepackage{xypic}\xymatrix{
{\mathop{\mathrm{Spec}_\mathbb{Z}} B} \ar[rr] \ar[dr]_{g^*} & & X \ar[dl]^\tau \\
& {\mathop{\mathrm{Spec}_\mathbb{Z}} k} &
} $](/blog/images/latex/200.png)
This gives the formula
The other way
In an attempt to go the other way, I looked for a map { -functors } { -functors with morphisms to }, but have been unable to find one. Let us more modestly restrict attention to affine schemes. Then there exists such a map, because the affine subcategories of both sides are dual to the category of -algebras, but I can’t find a way to describe the map in terms of functors of points.
Of course you could describe the map by first saying “construct the -algebra such that 
” (you can do this by ![$B = \mathop{\mathrm{Mor}}(X, \mathop{\mathrm{Spec}_k} k[t])$](/blog/images/latex/191.png)
)
but this is not very elegant, and doesn’t generalise to non-affine schemes, where I hope the correspondence still holds.
A serious obstacle to a nicer description of this map seems to be that 
has a single 
-point for every -algebra , so getting the complicated functor out of this is not going to be straightforward.