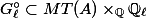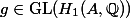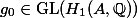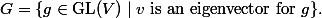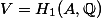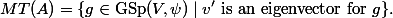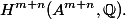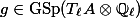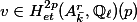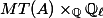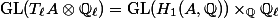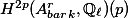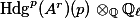Maths > Abelian varieties > Absolute Hodge classes
Deligne's Principle A and the Mumford-Tate conjecture
Posted by Martin Orr on Wednesday, 10 September 2014 at 11:20
In this post I will fill in a missing detail from two weeks ago, where I mentioned that the Mumford-Tate group is determined by the Hodge classes.
More precisely, I will show that an element 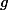
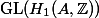
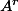 is an eigenvector of
is an eigenvector of 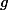 .
In the context of Deligne's theorem on absolute Hodge classes, this is known as Principle A.
.
In the context of Deligne's theorem on absolute Hodge classes, this is known as Principle A.
We will also see that a version of this statement holds for the  -adic monodromy group and Tate classes.
This implies a link between the Hodge, Tate and Mumford-Tate conjectures.
-adic monodromy group and Tate classes.
This implies a link between the Hodge, Tate and Mumford-Tate conjectures.
Characterisation of the Mumford-Tate group in terms of Hodge classes
Let  be an abelian variety over
be an abelian variety over  .
.
We saw previously that an element of 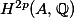 is a Hodge class if and only if it is an eigenvector for the Mumford-Tate group of
is a Hodge class if and only if it is an eigenvector for the Mumford-Tate group of  .
The obvious guess at a converse to this would be that an element
.
The obvious guess at a converse to this would be that an element 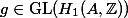
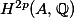
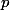 ) is an eigenvector of
) is an eigenvector of 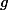 .
However this turns out to be false.
.
However this turns out to be false.
To recognise exactly which 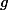
 .
Observe that
.
Observe that 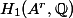
 copies of
copies of 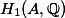
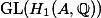
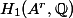
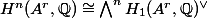
Using these actions, we can state and prove the following.
Theorem. An element
is in the Mumford-Tate group ofif and only if every Hodge class
(for every
and
) is an eigenvector of
.
Proof. The part we have to prove is that if every Hodge class
(for every
and
) is an eigenvector of
, then.
We will prove this using Chevalley's theorem on algebraic subgroups:
Theorem. Let
be an algebraic subgroup. Then there exist nonnegative integers
and a vector
such that
Of course we will apply this with
and.
But first we recall that
where
is a polarisation. As representations of
,
is isomorphic to
where
is the character telling us how
changes
.
Tensoring with the character
does not change which vectors are eigenvectors (only the characters associated with those eigenvectors) so applying the isomorphism of
-representations
, we can get
such that
By the Künneth formula,
is a sub-
-representation of
Thus we can regard
as a class in
. By construction
is an eigenvector for
, so it is a Hodge class. Thus, by main hypothesis of the theorem,
is an eigenvector for
.
We also know that the polarisation
is a Hodge class of weight 1 and hence, by hypothesis, an eigenvector for
. In other words
. We conclude that
satisfies the condition of (*) to be in
, as required.
Characterisation of the  -adic monodromy group in terms of Tate classes
-adic monodromy group in terms of Tate classes
Now let  be an abelian variety defined over a finitely generated field.
Similarly to above, we can prove:
be an abelian variety defined over a finitely generated field.
Similarly to above, we can prove:
Theorem. An element
is in the-adic algebraic monodromy group of
if and only if every Tate class
(for everyand
) is fixed by
.
This requires a little more work to prove than the statement about Hodge classes, because not every eigenvector of the  -adic monodromy group is a Tate class but only those eigenvectors with eigenvalue 1.
They key point is that, if
-adic monodromy group is a Tate class but only those eigenvectors with eigenvalue 1.
They key point is that, if 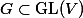 is reductive, then we can extend Chevalley's theorem to say that there is some
is reductive, then we can extend Chevalley's theorem to say that there is some 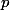 and some
and some 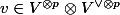
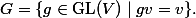
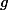 fix
fix  rather than just having
rather than just having  as an eigenvector, and
as an eigenvector, and 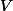 and
and 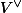 are raised to the same tensor power.)
are raised to the same tensor power.)
The fact that the  -adic algebraic monodromy group
-adic algebraic monodromy group 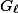
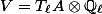
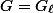
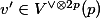
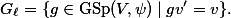
We can regard 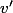 as an element of
as an element of 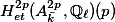
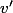 is a Tate class, and we can apply the same argument as before to conclude that, if
is a Tate class, and we can apply the same argument as before to conclude that, if
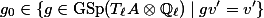
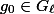
We can also modify the above theorem, replacing the  -adic algebraic monodromy group by its identity component and Tate classes by potentially Tate classes.
-adic algebraic monodromy group by its identity component and Tate classes by potentially Tate classes.
The Mumford-Tate conjecture
Now we focus on abelian varieties defined over a number field  (with a chosen embedding into
(with a chosen embedding into  ).
Recall the statement of the Mumford-Tate conjecture.
).
Recall the statement of the Mumford-Tate conjecture.
Mumford-Tate conjecture. The identity component
of the-adic algebraic monodromy group is equal to
(as subgroups of).
Using the above characterisations of 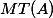 and
and 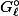 , this is equivalent to the following.
, this is equivalent to the following.
Conjecture. For every
and
, the subspace of potentially Tate classes in
is equal to.
The Hodge conjecture says that the space of Hodge classes is equal to the  -span of algebraic cycle classes, and the Tate conjecture says that the space of potentially Tate classes is equal to the
-span of algebraic cycle classes, and the Tate conjecture says that the space of potentially Tate classes is equal to the 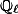
Note that the last paragraph requires one additional fact we have not mentioned before.
The Hodge conjecture concerns classes of algebraic cycles defined over  while the Tate conjecture (in its potentially Tate classes version) concerns classes of algebraic cycles defined over
while the Tate conjecture (in its potentially Tate classes version) concerns classes of algebraic cycles defined over 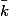 .
Fortunately this does not matter because if
.
Fortunately this does not matter because if 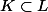 are algebraically closed fields,
are algebraically closed fields,  is a variety defined over
is a variety defined over  , and
, and 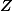 is a subvariety of
is a subvariety of  defined over
defined over  , then there exists a subvariety
, then there exists a subvariety 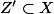 defined over
defined over  which is algebraically equivalent to
which is algebraically equivalent to 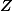 .
Algebraically equivalent varieties are mapped to the same cohomology class by the cycle class map (into any Weil cohomology theory).
.
Algebraically equivalent varieties are mapped to the same cohomology class by the cycle class map (into any Weil cohomology theory).
Deligne's theory of absolute Hodge classes, which I intend to discuss in my next posts, proves that every Hodge class on an abelian variety is a potentially Tate class.
This is half of the Mumford-Tate conjecture and allows us to conclude that, for an abelian variety,