Maths > Algebraic geometry > Functor of points
Affine k-schemes
Posted by Martin Orr on Friday, 25 September 2009 at 15:45
In my last post on functors of points, I showed that functor of points of an affine 
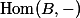







Note: throughout this post, all Hom-functors are on the category of 

Categorical definition
Recall that there is a dual equivalence between the category of affine 





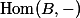
On the algebraic side, the restriction to "finitely-generated integral-domain" seems unnecessary. 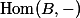
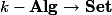


So we shall expand our universe of algebraic-geometric objects to include an object called 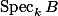


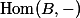

You might say that I haven't really defined anything, but the ethos behind this series of blog posts is that the functor of points is enough to define any algebraic-geometric object. After all, the usual way to define a geometric object is to start with a set of "points" making up the object. And here I have told you not just one set of points of 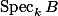



(Note: If you know some commutative algebra or have studied schemes, then the name 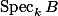
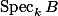
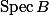



Concrete interpretation
I have defined the set of 
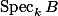

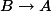
Recall the idea that we started with in my first post, that the functor of points of an affine variety tells you solutions to some fixed polynomial equations over a varying ring. The same thing still holds for affine 

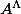


As an example, I shall compare ![X = \mathop{\mathrm{Spec}_\mathbb{C}} \mathbb{C}[x]/(x)](http://www.martinorr.name/blog/images/mathtex/229.png)
![Y = \mathop{\mathrm{Spec}_\mathbb{C}} \mathbb{C}[x]/(x^2)](http://www.martinorr.name/blog/images/mathtex/230.png)

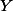
Now both of these have the same set of 
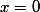
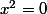

![\mathbb{C}[x]/(x)](http://www.martinorr.name/blog/images/mathtex/234.png)
![\mathbb{C}[x]/(x^2)](http://www.martinorr.name/blog/images/mathtex/235.png)


![\mathbb{C}[x]/(x^2) \to \mathbb{C}](http://www.martinorr.name/blog/images/mathtex/236.png)


However we can look at points of 
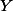

![A = \mathbb{C}[\varepsilon]/(\varepsilon^2)](http://www.martinorr.name/blog/images/mathtex/239.png)


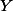
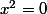
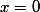

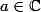

![\mathbb{C}[x]/(x^2) \to \mathbb{C}[\varepsilon]/(\varepsilon^2)](http://www.martinorr.name/blog/images/mathtex/242.png)
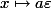
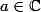
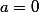
Good stuff.
Except there's a bug at the end. Y has a lot more than two A-points. It's got a whole family parametrised by C: x^2 = 0 admits ae as a solution, for any a in C.
Geometrically speaking, your "double point" Y manifests itself as being something like a point with a baby one-dimensional tangent space strapped onto it. You're really considering scheme maps from Y into Y when you take A-points.
Such a scheme map consists of a map on "honest points" (which is the unique map of singleton sets) plus a map on the tangent spaces. This is a map C --> C, and such maps are basically the same thing as complex numbers.
I'm sure there's some geometric intuition I'm neglecting to tell you, but that's a start.
That's a rather embarrassing mistake! Thanks for pointing it out. I've fixed it now.