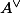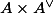Martin Orr's Blog

Line bundles and morphisms to the dual variety

Posted by Martin Orr on Saturday, 28 May 2011 at 15:25

Over the complex numbers, the dual of an abelian variety A is defined to have a Hodge structure dual to that of A. Hence morphisms A \to A^\vee can be interpreted as bilinear forms on the Hodge structure of A. Of particular importance are the morphisms corresponding to Hodge symplectic forms.

Last time we saw that A^\vee can also be interpreted as a group of line bundles on A. Today we will use this interpretation to define morphisms \phi_\mathcal{L} : A \to A^\vee which turn out to be the same as those corresponding to Hodge symplectic forms. Then we generalise the definition of \phi_\mathcal{L} to base fields other than \mathbb{C}, which we will use next time in constructing dual abelian varieties over number fields.

2 comments Tags abelian-varieties, alg-geom, hodge, maths Read more...

Dual abelian varieties and line bundles

Posted by Martin Orr on Monday, 09 May 2011 at 14:30

The definition I gave last time of dual abelian varieties was very much dependent on complex analytic methods. In this post I will explain how dual varieties can be interpreted geometrically: the points of A^\vee correspond to a certain group of line bundles on A. We construct a single line bundle \mathcal{P} on the product A \times A^\vee, the Poincaré bundle, such that all line bundles on A arise as restrictions of \mathcal{P}, and show that the pair (A^\vee, \mathcal{P}) satisfies a universal property.

no comments Tags abelian-varieties, alg-geom, hodge, maths Read more...

Archives