Vector extensions of abelian varieties
Posted by Martin Orr on Thursday, 17 April 2014 at 18:12
A theme of my posts on abelian varieties has been ad hoc constructions of objects which are equivalent to the (co)homology of abelian varieties together with their appropriate extra structures -- the period lattice for singular homology and the Hodge structure, the Tate module for 
-adic cohomology and its Galois representation. I want to do the same thing for de Rham cohomology. To prepare for this, I need to discuss vector extensions of abelian varieties -- that is extensions of abelian varieties by vector groups.
In this post I will define and classify extensions of an abelian variety by the additive group.
We will conclude that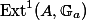 
, the set of isomorphism classes of such extensions, forms a vector space isomorphic to the tangent space of the dual of 
.
Most of this was discovered by Rosenlicht in the 1950s.