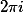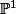Absolute Hodge classes in l-adic cohomology
Posted by Martin Orr on Friday, 26 June 2015 at 11:30
We can define absolute Hodge classes in 
-adic cohomology in the same way as absolute Hodge classes in de Rham cohomology.
We can then prove Deligne's theorem, that Hodge classes on an abelian variety are absolute Hodge, for -adic cohomology.
Because it is easy to prove that absolute Hodge classes in -adic cohomology are potentially Tate classes, this implies half of the Mumford-Tate conjecture.
In particular, it implies that if 
is an abelian variety over a number field, then a finite index subgroup of the image of the -adic Galois representation on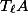 
is contained in the 
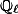-points of the Mumford-Tate group of .
This is the goal I have been working towards for some time on this blog.
Deligne's definition of absolute Hodge classes considered -adic cohomology (for all ) and de Rham cohomology simultaneously.
The accounts I read of this theory focussed on the de Rham side, leading me to believe that the de Rham part was essential and the -adic part an optional extra.
This is why I wrote the past few posts about de Rham cohomology and am now adding the -adic version on at the end, even though I am more interested in the -adic version.
Now that I understand what is going on, I realise that I could have used only
Before the main part of this post, talking about absolute Hodge classes in -adic cohomology, I need to talk about Tate twists in -adic cohomology.
These are more significant than Tate twists in singular cohomology because they change the Galois representations involved.
This resulted in some mistakes in my previous posts on Tate classes, which I think I have now fixed.
