Posted by Martin Orr on
Wednesday, 10 September 2014 at 11:20
In this post I will fill in a missing detail from two weeks ago, where I mentioned that the Mumford-Tate group is determined by the Hodge classes.
More precisely, I will show that an element 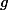
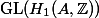
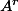 is an eigenvector of
is an eigenvector of 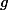 .
In the context of Deligne's theorem on absolute Hodge classes, this is known as Principle A.
.
In the context of Deligne's theorem on absolute Hodge classes, this is known as Principle A.
We will also see that a version of this statement holds for the  -adic monodromy group and Tate classes.
This implies a link between the Hodge, Tate and Mumford-Tate conjectures.
-adic monodromy group and Tate classes.
This implies a link between the Hodge, Tate and Mumford-Tate conjectures.
Tags
abelian-varieties, alg-geom, alg-groups, hodge, maths, number-theory
Read more...
Posted by Martin Orr on
Tuesday, 02 September 2014 at 19:30
In my last post I talked about Hodge classes on abelian varieties.
Today I will talk about the analogue in  -adic cohomology, called Tate classes.
Tate classes are defined to be classes in a Tate twist of the
-adic cohomology, called Tate classes.
Tate classes are defined to be classes in a Tate twist of the 
The Tate classes on a variety change if we extend the base field (because this changes the Galois group).
They are mainly interesting in the case in which the base field is finitely generated.
In this post I will also define potentially Tate classes, which depend less strongly on the base field (they are unchanged by finite extensions).
I will state the Tate conjecture, the  -adic analogue of the Hodge conjecture, which says that if the base field is finitely generated, then the vector space of Tate classes is spanned by classes of algebraic cycles.
I will also mention some other conjectures which are implied by or equivalent to the Tate conjecture or a slight strengthening of it.
-adic analogue of the Hodge conjecture, which says that if the base field is finitely generated, then the vector space of Tate classes is spanned by classes of algebraic cycles.
I will also mention some other conjectures which are implied by or equivalent to the Tate conjecture or a slight strengthening of it.
Unlike in the case of Hodge classes, we cannot easily ignore the Tate twist in the definition of Tate classes.
This post only contains brief remarks on Tate twists; there is a link to a later post with a more detailed discussion.
Tags
abelian-varieties, alg-geom, maths, number-theory
Read more...
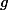
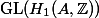
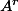 is an eigenvector of
is an eigenvector of 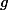 .
In the context of Deligne's theorem on absolute Hodge classes, this is known as Principle A.
.
In the context of Deligne's theorem on absolute Hodge classes, this is known as Principle A. -adic monodromy group and Tate classes.
This implies a link between the Hodge, Tate and Mumford-Tate conjectures.
-adic monodromy group and Tate classes.
This implies a link between the Hodge, Tate and Mumford-Tate conjectures.