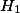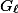Posted by Martin Orr on
Tuesday, 26 April 2011 at 12:35
In this post I will define dual abelian varieties over the complex numbers.
The motivation is that polarisations can be interpreted as isogenies from an abelian variety to its dual.
For the moment, all this is tied to Hodge structures so only works over the complex numbers,
but this is the view of polarisations which will we will generalise later to other fields.
Tags
abelian-varieties, alg-geom, hodge, maths
Read more...
Posted by Martin Orr on
Saturday, 26 March 2011 at 16:07
Last time, we defined polarisations on 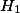







This is long, even though I have left out all the messy calculations. For full details, see Mumford's Abelian Varieties or Birkenhake-Lange's Complex Abelian Varieties.
For the next post, you will only need to know the two statements labelled as theorems.
This theorem is a special case of the Kodaira Embedding Theorem, which tells you that any compact complex manifold is projective if it has a polarisation, but that is somewhat more difficult.
Tags
abelian-varieties, alg-geom, hodge, maths
Read more...
Posted by Martin Orr on
Saturday, 26 February 2011 at 18:27
In the last post, I discussed Hodge symplectic forms.
Now I shall show that the 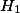
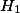
Tags
abelian-varieties, alg-geom, hodge, maths
Read more...
Posted by Martin Orr on
Saturday, 18 December 2010 at 15:00
Both the Hodge structure and the Tate module of an abelian variety come with symplectic forms which are (almost) preserved by the action of the relevant group (Mumford-Tate or Galois group).
The form on the Tate module, called the Weil pairing, will require some preparation.
So in this post I will construct the Hodge symplectic forms (also called the Riemann forms) on the Hodge structure.
Next time I will discuss some further properties of Hodge forms.
Tags
abelian-varieties, alg-geom, hodge, maths
Read more...
Posted by Martin Orr on
Saturday, 27 November 2010 at 16:22
In this post, I will continue to talk about the 
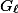
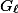
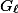
Tags
abelian-varieties, alg-geom, alg-groups, hodge, maths
Read more...