Posted by Martin Orr on
Friday, 26 June 2015 at 11:30
We can define absolute Hodge classes in  -adic cohomology in the same way as absolute Hodge classes in de Rham cohomology.
We can then prove Deligne's theorem, that Hodge classes on an abelian variety are absolute Hodge, for
-adic cohomology in the same way as absolute Hodge classes in de Rham cohomology.
We can then prove Deligne's theorem, that Hodge classes on an abelian variety are absolute Hodge, for  -adic cohomology.
Because it is easy to prove that absolute Hodge classes in
-adic cohomology.
Because it is easy to prove that absolute Hodge classes in  -adic cohomology are potentially Tate classes, this implies half of the Mumford-Tate conjecture.
-adic cohomology are potentially Tate classes, this implies half of the Mumford-Tate conjecture.
In particular, it implies that if  is an abelian variety over a number field, then a finite index subgroup of the image of the
is an abelian variety over a number field, then a finite index subgroup of the image of the  -adic Galois representation on
-adic Galois representation on 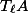 is contained in the
is contained in the 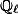 -points of the Mumford-Tate group of
-points of the Mumford-Tate group of  .
This is the goal I have been working towards for some time on this blog.
.
This is the goal I have been working towards for some time on this blog.
Deligne's definition of absolute Hodge classes considered  -adic cohomology (for all
-adic cohomology (for all  ) and de Rham cohomology simultaneously.
The accounts I read of this theory focussed on the de Rham side, leading me to believe that the de Rham part was essential and the
) and de Rham cohomology simultaneously.
The accounts I read of this theory focussed on the de Rham side, leading me to believe that the de Rham part was essential and the  -adic part an optional extra.
This is why I wrote the past few posts about de Rham cohomology and am now adding the
-adic part an optional extra.
This is why I wrote the past few posts about de Rham cohomology and am now adding the  -adic version on at the end, even though I am more interested in the
-adic version on at the end, even though I am more interested in the  -adic version.
Now that I understand what is going on, I realise that I could have used only
-adic version.
Now that I understand what is going on, I realise that I could have used only 

Before the main part of this post, talking about absolute Hodge classes in  -adic cohomology, I need to talk about Tate twists in
-adic cohomology, I need to talk about Tate twists in  -adic cohomology.
These are more significant than Tate twists in singular cohomology because they change the Galois representations involved.
This resulted in some mistakes in my previous posts on Tate classes, which I think I have now fixed.
-adic cohomology.
These are more significant than Tate twists in singular cohomology because they change the Galois representations involved.
This resulted in some mistakes in my previous posts on Tate classes, which I think I have now fixed.
Tags
abelian-varieties, alg-geom, hodge, maths, number-theory
Read more...
Posted by Martin Orr on
Friday, 19 June 2015 at 19:30
Tate twists in singular cohomology are a device for dealing with factors of 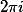
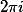
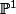
In the case of singular cohomology, Tate twists are largely a matter of normalising things conveniently.
Without them, we could just write out factors of 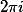 everywhere.
On the other hand, there is also a notion of Tate twists for
everywhere.
On the other hand, there is also a notion of Tate twists for  -adic cohomology, which cannot be omitted so easily, and which I will discuss in a subsequent post.
-adic cohomology, which cannot be omitted so easily, and which I will discuss in a subsequent post.
Tags
abelian-varieties, alg-geom, hodge, maths
Read more...
Posted by Martin Orr on
Thursday, 22 January 2015 at 11:10
As I explained last time, one of the key steps in the the proof of Deligne's theorem on absolute Hodge classes is Principle B.
This allows us to take an absolute Hodge classes on one fibre in a family of varieties, and deduce that certain classes are absolute Hodge on other fibres of the same family.
In this post I shall explain a proof of Principle B due to Blasius, which I think is simpler than Deligne's original proof.
As I also mentioned last time, one can state Principle B in a number of slightly different forms.
I have chosen to use the following version instead of the one I gave last time (where there was a lot hidden in the mention of the Gauss-Manin connection, which I am happy not to have to talk about).
This version can be applied to Shimura varieties just as easily, or even more easily, than the previous one.
Theorem. Let 




If there is a point 





Tags
abelian-varieties, alg-geom, hodge, maths
Read more...
Posted by Martin Orr on
Wednesday, 17 December 2014 at 19:00
Today I will outline the proof of Deligne's theorem that Hodge classes on an abelian variety are absolute Hodge.
The proof goes through three steps of reducing to increasingly special types of abelian varieties, until finally one reaches a case where it is easy to finish off.
This post has ended up longer than usual, but I don't think it is worth splitting into two.
A key ingredient is Deligne's Principle B, which is used for two of the three reduction steps.
Principle B says that if we have a family of varieties  and a flat section of the relative de Rham cohomology bundle
and a flat section of the relative de Rham cohomology bundle 
 , then in fact it is absolute Hodge everywhere.
This means that, if we have a method for constructing suitable families of abelian varieties and sections of their relative de Rham cohomology, then we only have to prove that Hodge classes are absolute Hodge at one point of each relevant family.
We use Shimura varieties to construct these families of abelian varieties on which to apply Principle B.
, then in fact it is absolute Hodge everywhere.
This means that, if we have a method for constructing suitable families of abelian varieties and sections of their relative de Rham cohomology, then we only have to prove that Hodge classes are absolute Hodge at one point of each relevant family.
We use Shimura varieties to construct these families of abelian varieties on which to apply Principle B.
The outline of the proof looks like this:
- Reduce to Hodge classes on abelian varieties of CM type (using Principle B)
- Reduce to a special type of Hodge classes, called Weil classes, on a special type of abelian variety, called abelian varieties of split Weil type (using linear algebra)
- Reduce to Hodge classes on abelian varieties which are isogenous to a power of an elliptic curve (using Principle B)
- Observe that it is easy to prove Deligne's theorem (and indeed the Hodge conjecture) for abelian varieties which are isogenous to a power of an elliptic curve
Tags
abelian-varieties, alg-geom, hodge, maths, shimura-varieties
Read more...
 -adic cohomology in the same way as absolute Hodge classes in de Rham cohomology.
We can then prove Deligne's theorem, that Hodge classes on an abelian variety are absolute Hodge, for
-adic cohomology in the same way as absolute Hodge classes in de Rham cohomology.
We can then prove Deligne's theorem, that Hodge classes on an abelian variety are absolute Hodge, for  -adic cohomology.
Because it is easy to prove that absolute Hodge classes in
-adic cohomology.
Because it is easy to prove that absolute Hodge classes in  -adic cohomology are potentially Tate classes, this implies half of the Mumford-Tate conjecture.
-adic cohomology are potentially Tate classes, this implies half of the Mumford-Tate conjecture. is an abelian variety over a number field, then a finite index subgroup of the image of the
is an abelian variety over a number field, then a finite index subgroup of the image of the  -adic Galois representation on
-adic Galois representation on 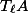 is contained in the
is contained in the 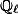 -points of the Mumford-Tate group of
-points of the Mumford-Tate group of  .
This is the goal I have been working towards for some time on this blog.
.
This is the goal I have been working towards for some time on this blog. -adic cohomology (for all
-adic cohomology (for all  ) and de Rham cohomology simultaneously.
The accounts I read of this theory focussed on the de Rham side, leading me to believe that the de Rham part was essential and the
) and de Rham cohomology simultaneously.
The accounts I read of this theory focussed on the de Rham side, leading me to believe that the de Rham part was essential and the  -adic part an optional extra.
This is why I wrote the past few posts about de Rham cohomology and am now adding the
-adic part an optional extra.
This is why I wrote the past few posts about de Rham cohomology and am now adding the  -adic version on at the end, even though I am more interested in the
-adic version on at the end, even though I am more interested in the  -adic version.
Now that I understand what is going on, I realise that I could have used only
-adic version.
Now that I understand what is going on, I realise that I could have used only 

 -adic cohomology, I need to talk about Tate twists in
-adic cohomology, I need to talk about Tate twists in  -adic cohomology.
These are more significant than Tate twists in singular cohomology because they change the Galois representations involved.
This resulted in some mistakes in my previous posts on Tate classes, which I think I have now fixed.
-adic cohomology.
These are more significant than Tate twists in singular cohomology because they change the Galois representations involved.
This resulted in some mistakes in my previous posts on Tate classes, which I think I have now fixed.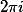











 and a flat section of the relative de Rham cohomology bundle
and a flat section of the relative de Rham cohomology bundle 










