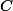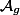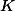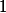Posted by Martin Orr on
Friday, 30 March 2012 at 12:20
I wanted to write a post about the Masser-Wüstholz isogeny theorem, which gives a quantitative version of Finiteness Theorem I.
But it turned out to be too long so for today I will focus on the main ingredient in the proof of the isogeny theorem: the Masser-Wüstholz period theorem.
The period theorem gives a bound for the degree of the smallest abelian subvariety of a fixed abelian variety 

Period Theorem. (Masser, Wüstholz 1993) Let 

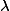


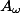


![\deg_\lambda A_\omega \leq C \max([k:\mathbb{Q}], h_F(A), H_\lambda(\omega, \omega))^\kappa](http://www.martinorr.name/blog/images/mathtex/1256.png)
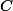
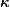

Masser and Wüstholz gave a value for 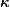
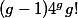
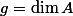
Tags
abelian-varieties, alg-geom, maths, number-theory
Read more...
Posted by Martin Orr on
Saturday, 31 December 2011 at 15:31
In this post I shall give the definition of the Faltings height of an abelian variety over any number field.
Last time we did this over 

Tags
abelian-varieties, alg-geom, faltings, maths, number-theory
Read more...
Posted by Martin Orr on
Thursday, 17 November 2011 at 15:58
The Faltings height is a real number attached to an abelian variety (defined over a number field), which is at the centre of Faltings' proof of Finiteness Theorem I.
In this post all I will do is define the Faltings height of an abelian variety over 
For an abelian variety 




Faltings' proof of Finiteness I proceeds by showing that for any fixed number field, there are finitely many abelian varieties of bounded Faltings height.
This is done by showing that the Faltings height is not far away from the classical height of a point representing the abelian variety in the moduli space 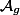
Tags
abelian-varieties, alg-geom, faltings, maths, number-theory
Read more...
Posted by Martin Orr on
Monday, 19 September 2011 at 16:34
Faltings famously proved the Mordell, Shafarevich and Tate conjectures in 1983.
In this post I will discuss the relationships between the Tate and Shafarevich conjectures and some other finiteness theorems for abelian varieties.
Everything which I call a conjecture in this post is known to be true:
they all follow from Finiteness Theorem I.
Proving Finiteness Theorem I was the bulk of Faltings' work, but I am not going to talk about that today.
Finiteness Theorem I.
Given a number field 


Tags
abelian-varieties, alg-geom, faltings, maths, number-theory
Read more...


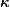
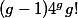
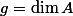
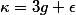

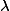

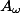
![\deg_\lambda A_\omega \leq C \max([k:\mathbb{Q}], h_F(A), H_\lambda(\omega, \omega))^\kappa](http://www.martinorr.name/blog/images/mathtex/1256.png)