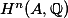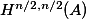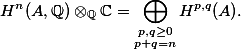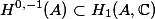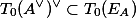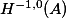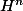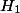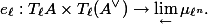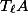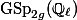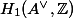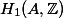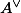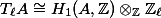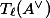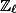Martin Orr's Blog

Hodge classes on abelian varieties

Posted by Martin Orr on Monday, 25 August 2014 at 18:50

In this post I will define Hodge classes and state the Hodge conjecture. I will restrict my attention to the case of abelian varieties and say the minimum amount necessary to be able to discuss the relationships between the Hodge, Tate and Mumford-Tate conjectures and absolute Hodge classes in subsequent posts. There are many excellent accounts of this material already written, which may give greater detail and generality.

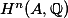
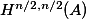
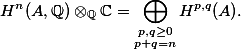
Hodge classes are cohomology classes on a complex variety A which are in the intersection of the singular cohomology H^n(A, \mathbb{Q}) and the middle component H^{n/2,n/2}(A) of the Hodge decomposition H^n(A, \mathbb{Q}) \otimes_\mathbb{Q} \mathbb{C} = \bigoplus_{\substack{p,q\geq 0 \\ p+q=n}} H^{p,q}(A). They can also be defined as rational cohomology classes which are eigenvectors for the Mumford-Tate group. The Hodge conjecture predicts that these classes are precisely the \mathbb{Q}-span of cohomology classes coming from algebraic subvarieties of A.

no comments Tags abelian-varieties, alg-geom, hodge, maths Read more...

The Hodge filtration and universal vector extensions

Posted by Martin Orr on Friday, 13 June 2014 at 20:10

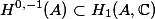
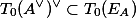
We will begin this post by looking at the isomorphism between the Hodge filtration H^{0,-1}(A) \subset H_1(A, \mathbb{C}) of a complex abelian variety A and the natural filtration T_0(A^\vee)^\vee \subset T_0(E_A) on the tangent space to the universal vector extension of A.

The significance of this isomorphism is that the Hodge filtration, as we defined it before, is constructed by transcendental methods, valid only over \mathbb{C}, but the universal vector extension is an object of algebraic geometry. So this gives us an analogue for the Hodge filtration for abelian varieties over any base field. Furthermore, in the usual way of algebraic geometry, the construction of the universal vector extension can be carried out uniformly in families of abelian varieties.

We will use the construction of the universal vector extension in families to show that “the Hodge filtration varies algebraically in families.” We will first have to explain what this statement means. We will also mention briefly why 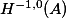H^{-1,0}(A) does not vary algebraically.

A note on the general philosophy of this post: the usual construction of an algebraic-geometric object isomorphic to the Hodge filtration uses de Rham cohomology, which works for 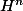H^n of an arbitrary smooth projective variety. My aim in using universal vector extensions is to give an ad hoc construction of de Rham (co)homology, valid only for H_1 of an abelian variety, requiring less sophisticated technology than the general construction. This fits with previous discussion on this blog of the Hodge structure on H_1, constructed via the exponential map from the tangent space of A, and of the \ell-adic H_1, constructed as the Tate module.

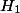
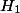
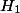
no comments Tags abelian-varieties, alg-geom, hodge, maths Read more...

Weil pairings: the skew-symmetric pairing

Posted by Martin Orr on Tuesday, 06 September 2011 at 13:52

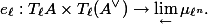
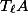
Last time, we defined a pairing e_\ell : T_\ell A \times T_\ell (A^\vee) \to \lim_\leftarrow \mu_{\ell^n}. By composing this with a polarisation, we get a pairing of T_\ell A with itself. This pairing is symplectic; the proof of this will occupy most of the post.

We will also see that the action of the Galois group on this pairing is given by the (inverse of the) cyclotomic character, as I promised a long time ago (in the comments). This tells us that the image of the \ell-adic Galois representation of A is contained in \operatorname{GSp}_{2g}(\mathbb{Q}_\ell). This is the end of my series on Mumford-Tate groups and \ell-adic representations attached to abelian varieties.

no comments Tags abelian-varieties, alg-geom, hodge, maths, number-theory Read more...

Weil pairings: definition

Posted by Martin Orr on Monday, 29 August 2011 at 17:27

Recall that for an abelian variety A over the complex numbers, H_1(A^\vee, \mathbb{Z}) is dual to H_1(A, \mathbb{Z}) (this is built in to the analytic definition of A^\vee). Since T_\ell A \cong H_1(A, \mathbb{Z}) \otimes_\mathbb{Z} \mathbb{Z}_\ell, this tells us that T_\ell(A^\vee) is dual to T_\ell A (as \mathbb{Z}_\ell-modules). We would like to show that this is true over other fields as well, which we will do by constructing the Weil pairings.

no comments Tags abelian-varieties, alg-geom, hodge, maths, number-theory Read more...

Dual varieties over general fields

Posted by Martin Orr on Friday, 24 June 2011 at 17:26

Today we will construct dual abelian varieties over number fields. We use the universal property from two posts ago to define dual abelian varieties, then we give a simple construction inspired by the complex case. Proving that this construction satisfies the universal property is harder; in the case of number fields, we will use Galois descent to deduce it from the complex case which we already know analytically.

2 comments Tags abelian-varieties, alg-geom, hodge, maths Read more...

1 2 3 4 5

Archives