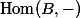Posted by Martin Orr on Friday, 25 September 2009 at 15:45
In my last post on functors of points, I showed that functor of points of an affine 
Posted by Martin Orr on Wednesday, 02 September 2009 at 22:51
In this article, I will examine in more detail the functor of points of an affine variety,
which I defined in the last article.
I shall show that this functor is the same as a Hom-functor on the category of
Posted by Martin Orr on Tuesday, 25 August 2009 at 20:56
I think I have made some progress recently in understanding the "functor of points" idea in algebraic geometry. In this article I shall explain how the functor of points of an affine variety arises simply by considering solutions to fixed polynomials over varying rings; this gives the motivating example for considering functors associated to more general algebraic-geometric objects.
Posted by Martin Orr on Friday, 19 June 2009 at 11:49
Hilbert's Nullstellensatz is an algebraic result fundamental to algebraic geometry. There are many different proofs of the Nullstellensatz. In this post I will consider the proof given in this year's Part III Commutative Algebra course, and in particular one section of the proof that seems to contain lots of magic. When I was revising for the exams, I realised that part of the mystery came from the fact that the particular theorem proved in Commutative Algebra does not require an algebraically closed field, unlike the standard statement of Hilbert's Nullstellensatz.
Thanks are due to Lloyd West for starting me thinking about this, and to Jon Nelson for giving me the courage to believe that it might be true and for supplying the proof of Lemma 4.
Posted by Martin Orr on Saturday, 16 May 2009 at 19:54
In my last post on the Yoneda lemma for groups, I ignored the naturality part of the lemma. I want to work in detail what this means once - it is a lot of fiddly composing of morphisms and I probably won't do it again (at least in public). If you're not in the mood for following such details, then there is little point in reading this, although you could skip to the last paragraph.