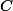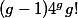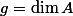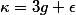Posted by Martin Orr on
Friday, 03 August 2012 at 11:06
Today I will explain how to prove the Masser-Wüstholz Period Theorem starting from the Key Proposition, an weaker existence result for abelian subvarieties of bounded degrees. The Key Proposition and the Tangent Space Lemma, which I mention briefly, are the main results proved by Masser and Wüstholz by the techniques of transcendental number theory on their way to the Period Theorem.
Recall that the Period Theorem is a bound for the degree of the smallest abelian subvariety of 





Tags
abelian-varieties, alg-geom, maths, number-theory
Read more...
Posted by Martin Orr on
Wednesday, 25 April 2012 at 14:09
Let 

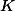

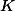

The Masser-Wüstholz isogeny theorem answers this question, at least subject to a minor condition on polarisations (I think that this was removed in a later paper of Masser and Wüstholz but it is not too important anyway -- when deducing Finiteness Theorem I you can remove the polarisation issue with Zarhin's Trick).
Theorem. (Masser, Wüstholz 1993) Let 

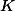
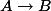
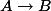
![c \max([K:\mathbb{Q}], h(A))^\kappa](http://www.martinorr.name/blog/images/mathtex/1196.png)


We will prove this using the Masser-Wüstholz period theorem which I discussed last time.
Tags
abelian-varieties, alg-geom, maths, number-theory
Read more...
Posted by Martin Orr on
Friday, 30 March 2012 at 12:20
I wanted to write a post about the Masser-Wüstholz isogeny theorem, which gives a quantitative version of Finiteness Theorem I.
But it turned out to be too long so for today I will focus on the main ingredient in the proof of the isogeny theorem: the Masser-Wüstholz period theorem.
The period theorem gives a bound for the degree of the smallest abelian subvariety of a fixed abelian variety 

Period Theorem. (Masser, Wüstholz 1993) Let 

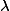


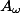


![\deg_\lambda A_\omega \leq C \max([k:\mathbb{Q}], h_F(A), H_\lambda(\omega, \omega))^\kappa](http://www.martinorr.name/blog/images/mathtex/1256.png)
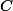
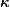

Masser and Wüstholz gave a value for 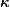
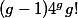
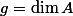
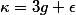
Tags
abelian-varieties, alg-geom, maths, number-theory
Read more...
Posted by Martin Orr on
Saturday, 31 December 2011 at 15:31
In this post I shall give the definition of the Faltings height of an abelian variety over any number field.
Last time we did this over 

Tags
abelian-varieties, alg-geom, faltings, maths, number-theory
Read more...






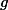


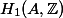


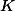


![\lvert \mathop{\mathrm{Im}} \tau_{ij} \rvert \leq c [K:\mathbb{Q}] \max(1, h(A)).](http://www.martinorr.name/blog/images/mathtex/1168.png)

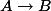
![c \max([K:\mathbb{Q}], h(A))^\kappa](http://www.martinorr.name/blog/images/mathtex/1196.png)
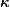

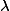
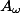
![\deg_\lambda A_\omega \leq C \max([k:\mathbb{Q}], h_F(A), H_\lambda(\omega, \omega))^\kappa](http://www.martinorr.name/blog/images/mathtex/1256.png)